排序类型
平均情况
最好情况
最坏情况
辅助空间
稳定性
冒泡排序
O(n²)
O(n)
O(n²)
O(1)
稳定
选择排序
O(n²)
O(n²)
O(n²)
O(1)
不稳定
直接插入排序
O(n²)
O(n)
O(n²)
O(1)
稳定
折半插入排序
O(n²)
O(n)
O(n²)
O(1)
稳定
希尔排序
O(n^1.3)
O(nlogn)
O(n²)
O(1)
不稳定
归并排序
O(nlog₂n)
O(nlog₂n)
O(nlog₂n)
O(n)
稳定
快速排序
O(nlog₂n)
O(nlog₂n)
O(n²)
O(nlog₂n)
不稳定
堆排序
O(nlog₂n)
O(nlog₂n)
O(nlog₂n)
O(1)
不稳定
计数排序
O(n+k)
O(n+k)
O(n+k)
O(k)
稳定
桶排序
O(n+k)
O(n+k)
O(n²)
O(n+k)
(不)稳定
基数排序
O(d(n+k))
O(d(n+k))
O(d(n+kd))
O(n+kd)
稳定
推荐文章:https://www.cnblogs.com/morethink/p/8419151.html#%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F
冒泡排序 原理:从第一个数开始,连续两个数取最大的那个数,然后最大的数和后面的数进行对比,在一轮循环后最大的数一定冒泡到最后,然后下一轮冒泡,最后的数就不用参与(因为最后的数经过冒泡后一定是这一轮最大的)、
实现:
for循环,因为是当前数和下一个数比较,最后一个数没有下一个,所以一共进行length - 1轮
每一次比较的都是前面没有排好的数字(0到(长度-经过排序的轮数也就是i)
如果当前数比后面的数大,进行交换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public class MaoPaoSort public static void main (String[] args) int arr[] = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; for (int i = 0 ; i < arr.length - 1 ; i++) { for (int j = 0 ; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } System.out.println(Arrays.toString(arr)); } }
优化冒泡排序 当数组中已经是有序数据,或者经过冒泡后已经使上面的数据变得有序,那么上面的程序还是会继续进行下去,进行无意义的比较
当一个数组变的有序的时候,那么在第二次比较的过程中一定不会发生交换,而数组无序的时候,在进行冒泡的时候一定会发生至少一次比较交换。
可以设置一个变量,来标记当前数组是否已经有序。
实现:
在冒泡排序的基础上,添加一个标志位flag
在第一个for循环中初始化
在第二个for循环全部结束后判断是否发生了交换,如果为发生交换则数组已经有序,跳出循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class MaoPaoSortPlus public static void main (String[] args) int arr[] = {-1 , -9 , 2 , 3 , 4 , 9 , 5 , 8 }; boolean flag=true ; for (int i = 0 ; i < arr.length - 1 ; i++) { flag=true ; for (int j = 0 ; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; flag = false ; } count++; } if (flag){ break ; } } System.out.println(Arrays.toString(arr)); } }
注意:
必须把flag=true放到第一次for循环内部,在没一轮冒泡前都要对flag进行一次初始化,因为可能经过上一轮数组已经变得有序,此时发生了交换flag = false,如果不对flag进行初始化,那么在下一轮之后一直都是false,就算已经排序好了未发生交换也不能跳出循环。
选择排序 原理:选择一轮中最小的那个数据,然后把最小的数据放到最开始的位置,这样在每一轮循环完毕后数组前面的数一定是本次循环中最小的那个数。
实现:
定义本轮循环开始的初始位置下标min(因为min个前面数字一定是最小的且已经是有序的)
for循环,因为是当前数和下一个数比较,最后一个数没有下一个,所以一共进行length - 1轮
获取当前开始下标i,min = i
for循环,初始值为i + 1,(自身和自身比较没有意义),循环到最后
如果中间有数据比minValue(arr[min])小,拿到这个下标j,min = j
在一轮循环结束后,交换min和本轮开始的最初下标i的位置,使本轮循环的最小数放到最前的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public class SelectSort public static void main (String[] args) int [] arr = {8 , -1 , 10 , 2 , -1 , 4 , -9 }; int min; int minValue; for (int i = 0 ; i < arr.length - 1 ; i++) { min = i; minValue = arr[i]; for (int j = i + 1 ; j < arr.length; j++) { if (minValue > arr[j]) { min = j; minValue = arr[j]; } } if (min != i) { int temp = arr[i]; arr[i] = arr[min]; arr[min] = temp; } } System.out.println(Arrays.toString(arr)); } }
和冒泡排序对比:
算法
原理
实现
交换次数
核心
冒泡排序
最大值放最后,每一轮最后的数一定是所有数里面最大的,数值对比后立马发生交换,最大的继续和下面的数比较
第一个数和后面的数比较,如果第一个数大则交换位置,大的数继续和下一位数比较一直到length-i;
每一轮比较都有可能发生(length-i-1)次交换
第i轮一定是,length-i个数里面最大的,最后i个数一定是整体有序
选择排序
最小值放最前,每一轮的第一个数一定是所有数里面最小的,数值对比后,记录最小值,在一轮结束后,最小值和开始的arr[i]交换
从i开始,选择最小的数,记录最小数的下标,一直到length;在一轮循环结束后,交换i和最小数的下标,把最小的数放在最前面;
在没一轮结束后,发生一次交换
第i轮一定是,ength-i个数里面最小 的,前面i个一定是整体有序
插入排序 原理:从第i个数开始,对前面的数进行比较,如果前面的数比arr[i]大则前面的数后移(或交换位置),继续和前面的数比较,直到前面的一位数小于arr[i],这样保证了每一轮前i个数是从小到大有序的,只需要给i这个数选择一个合适的位置
实现:
for循环从1开始到length,(如果发生比较次数都为lentth-1,无论是从0开始还是从1开始都可以实现算法,以为是和前面的发生比较,所以从1开始更好,如果和后面的发生比较,从0开始更好)
因为第一轮从1开始,第二次for循环从i开始,和前面的i发生比较,如果前面的值大于当前值,发生交换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class InsertSortWithExchange public static void main (String[] args) int arr[] = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; for (int i = 1 ; i < arr.length; i++) { for (int j = i; j > 0 ; j--) { if (arr[j] < arr[j -1 ]) { int temp = arr[j]; arr[j] = arr[j - 1 ]; arr[j - 1 ] = temp; } } } System.out.println(Arrays.toString(arr)); } }
实现:
for循环从1开始到length,(如果发生比较次数都为lentth-1,无论是从0开始还是从1开始都可以实现算法,以为是和前面的发生比较,所以从1开始更好,如果和后面的发生比较,从0开始更好)
因为第一轮从1开始,第二次for循环从i开始,和前面的i发生比较,如果前面的值大于当前值,发生较大的值向后移,最后结束的时候才交换位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class InsertSortWithInsert public static void main (String[] args) int arr[] = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; int min; int minValue; for (int i = 1 ; i < arr.length; i++) { min = i; minValue = arr[i]; for (int j = i; j > 0 ; j--) { if (minValue < arr[j - 1 ]) { arr[j] = arr[j-1 ]; min -- ; } } arr[min] = minValue; } System.out.println(Arrays.toString(arr)); } }
算法
原理
实现
交换次数
核心
冒泡排序
最大值放最后,每一轮最后的数一定是所有数里面最大 的,数值对比后立马发生交换,最大的继续和下面的数比较
第一个数和后面的数比较,如果第一个数大则交换位置,大的数继续和下一位数比较一直到length-i;
每一轮比较都有可能发生(length-i-1)次交换
第i轮一定是,length-i个数里面最大的,最后i个数一定是整体有序
选择排序
最小值放最前,每一轮的第一个数一定是所有数里面最小 的,数值对比后,记录最小值,在一轮结束后,最小值和开始的arr[i]交换
从i开始,选择最小的数,记录最小数的下标,一直到length;在一轮循环结束后,交换i和最小数的下标,把最小的数放在最前面;
在没一轮结束后,发生一次交换
第i轮一定是,ength-i个数里面最小 的,前面i个一定是整体有序
插入排序
最小值放全面卖弄,每一轮第一个数一定是本轮数最小 的
不确定
从i开始,保证i前面的数是本轮有序 的,最小的值向前移动
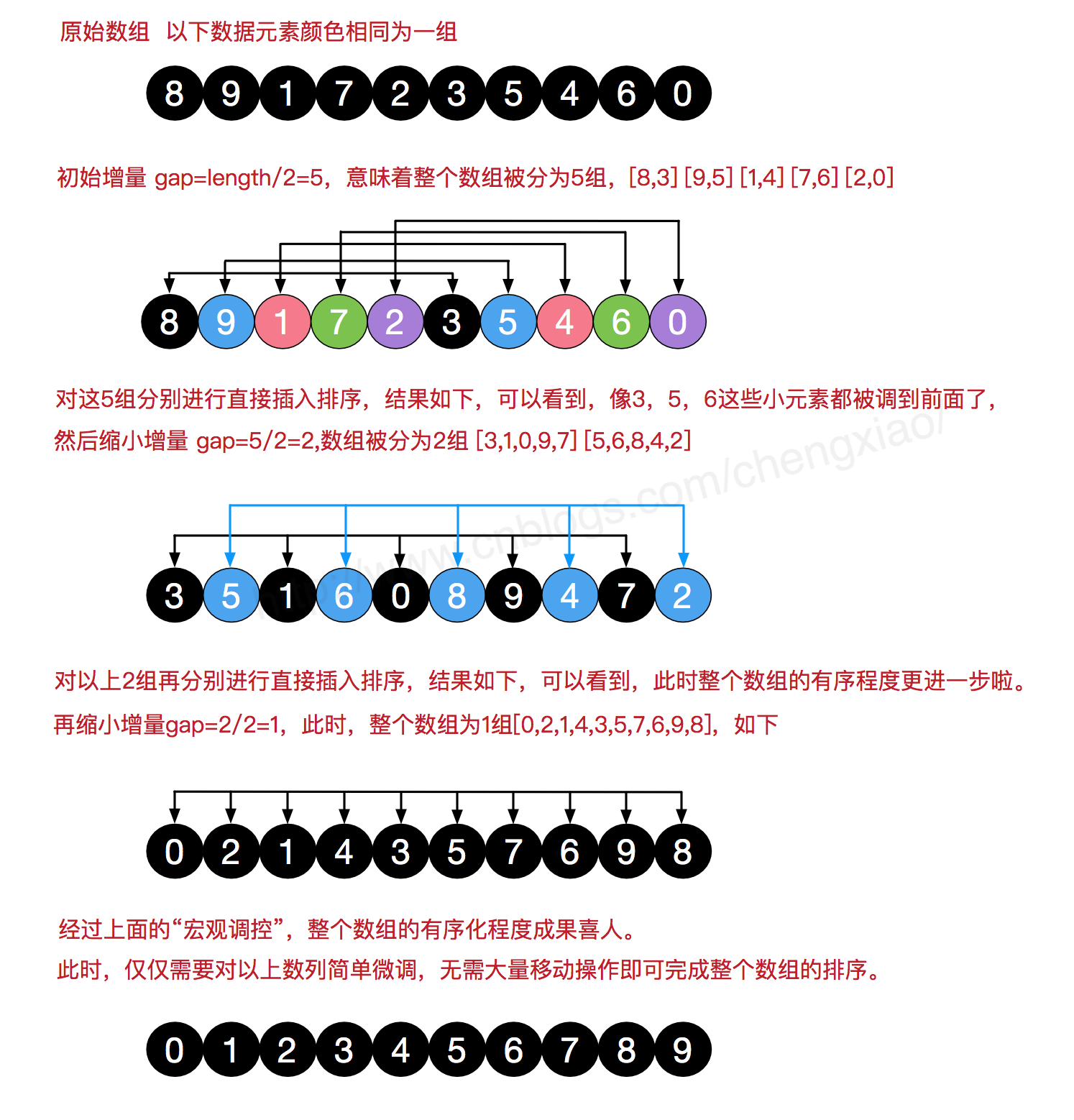
希尔排序 1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序 。
实现:
对数组划分步长,进行for循环每次的步长为数组总长度的1/2,直到步长小于0
对插入排序的直接使用,知识插入排序的步长为1,而希尔排序的步长是动态变化的
for循环,以步长为开始,步长后的第一个数开始比较
while循环,当前位置大于一个步长且与前面对此,minValue < arr[min - grap],则之前打的数后移
在一轮驯化结束后,把较小的数放回步长开始的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public class ShellSortWithInsert public static void main (String[] args) int arr[] = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; int min; int minValue; for (int grap = arr.length / 2 ; grap > 0 ; grap /= 2 ) { for (int i = grap; i < arr.length; i++) { min = i; minValue = arr[i]; while (min >= grap && minValue < arr[min - grap]) { arr[min] = arr[min - grap]; min -= grap; } arr[min] = minValue; } } System.out.println(Arrays.toString(arr)); } }
快速排序 原理:快速排序就是使用分治算法把一个序列分成为两个子序列。
从数列中挑出一个原色,称为“基准”
重新排序数列,所有比基准值小的元素排在基准面前,所有比基准大的元素摆在基准后面(相同的数可以放到任何一边)。在分区结束后,基准就处于数列的中间位置
递归的把小于基准元素的子数列和大于基准元素的子数列排序。
关键点:
如何把比基准值小的数放左边,比基准值大的数放右边
因为我们不知道小于基准值和大于基准值的数的数量,不能逐个遍历,所以我们换个思路,比基准值小的数放最左边,left++,比基准值大的数放最右边right–,最后当left==right的时候,说明整个数组已经遍历一遍了,整个left==right的位置就是基准值的位置。
(左右)双指针,从右端开始,如果右端值大于基准值,则右指针向左移动(保证右边的值大于基准值),如果发现右端值小于基准值,则把左指针值放在右指针位置;如果左端的值小于基准值,则左指针向右移动,如果左端的值大于基准值,则把右指针值放到左指针位置;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public class QuiteSort public static void main (String[] args) int [] arr = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; int [] sort = sort(arr, 0 , arr.length - 1 ); System.out.println(Arrays.toString(sort)); } public static int [] sort(int [] a, int low, int high) { if (low >= high) { return a; } int left = low; int right = high; int temp = a[left]; while (left < right) { while (left < right && a[right] >= temp) { right--; } a[left] = a[right]; while (left < right && a[left] <= temp) { left++; } a[right] = a[left]; } a[left] = temp; sort(a, low, left - 1 ); sort(a, left + 1 , high); return a; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class QuiteSort public static void main (String[] args) int [] arr = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; int [] sort = sort(arr, 0 , arr.length - 1 ); System.out.println(Arrays.toString(sort)); } public static int [] sort(int [] a, int low, int high) { if (low >= high) { return a; } int left = low; int right = high; int index = (int ) (Math.random() * (right - left) + left); int temp = nums[left]; nums[left] = nums[index]; nums[index] = temp; temp = nums[left]; while (left < right) { while (left < right && a[right] >= temp) { right--; } a[left] = a[right]; while (left < right && a[left] <= temp) { left++; } a[right] = a[left]; } a[left] = temp; sort(a, low, left - 1 ); sort(a, left + 1 , high); return a; } }
归并排序 原理:先将数组拆分知道不能拆分为两个为止(也就是最小是两个数为一组),然后对两个数排序,在一次合并
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 public class MergerSort public static void main (String[] args) int [] arr = {8 , 5 , 3 , 2 , -1 , 4 , -9 }; MergerSort mergerSort = new MergerSort(); int [] sort = mergerSort.sort(arr); System.out.println(Arrays.toString(sort)); } private static int [] aux; public int [] sort(int [] arr) { aux = new int [arr.length]; sort(arr, 0 , arr.length - 1 ); return arr; } public void sort (int [] arr, int low, int high) if (high <= low) { return ; } int mid = (low + high) / 2 ; sort(arr, low, mid); sort(arr, mid + 1 , high); merge(arr, low, mid, high); } private void merge (int [] arr, int low, int mid, int high) int left = low; int right = mid + 1 ; for (int i = low; i <= high; i++) { aux[i] = arr[i]; } for (int i = low; i <= high; i++) { if (left > mid) { arr[i] = aux[right++]; } else if (right > high) { arr[i] = aux[left++]; } else if (aux[right] < aux[left]) { arr[i] = aux[right++]; } else { arr[i] = aux[left++]; } } } }
基数排序 原理:将所有带比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从低位开始,一次进行一次排序。这样从最低位一直到最高位排序完成后,数列就变成有序数列
实现:
取得数组中的最大数,获取位数
arr为原始数组,从最低位开始去每个位组成radix长度
对radix进行计数排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 public class radixSort public static void main (String[] args) int [] arr = {8 , 5 , 3 , 2 , 1 , 4 , 9 , 20 , 362 }; int [] sort = sort(arr); System.out.println(Arrays.toString(sort)); } public static int [] sort(int [] arr) { if (arr.length <= 1 ) { return arr; } int max = arr[0 ]; for (int i = 1 ; i < arr.length; i++) { if (arr[i] > max) { max = arr[i]; } } int maxDigit = 1 ; while ((max /= 10 ) > 0 ) { maxDigit++; } int [][] buckets = new int [10 ][arr.length]; int [] bktLen = new int [10 ]; int base = 1 ; for (int i = 0 ; i < maxDigit; i++) { bktLen = new int [10 ]; for (int value : arr) { int bktValue = (value / base) % 10 ; buckets[bktValue][bktLen[bktValue]++] = value; } int index = 0 ; for (int j = 0 ; j < buckets.length; j++) { for (int k = 0 ; k < bktLen[j]; k++) { arr[index++] = buckets[j][k]; } } base *= 10 ; } return arr; } }
堆排序 计数排序 桶排序 java中arrys.sort的实现 核心算法是由插入排序算法完成了,如果长度大于32则将数组拆分为小的连续序列,然后对连续序列进行合并
在小规模的数据排序算法中,O(n^2)的排序算法并不一定比O(nlogn)的排序算法执行时间长。对于小数据量的排序,选择了比较简单,不需要递归的插入排序算法。
说一个常用的稳定的排序算法和适用场景 稳定的排序算法:冒泡排序、插入排序、归并排序、基数排序
基数排序适用于对时间、字符串这些数据(能够分割出独立的位,而且位之间具有明显的递进关系,且位之间的范围不是太大)
时间复杂度为nlog2n的排序算法有哪些 归并、快排、堆排