题目 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示例 1 : 输入:coins = [1 , 2 , 5 ], amount = 11 输出:3 解释:11 = 5 + 5 + 1 示例 2 : 输入:coins = [2 ], amount = 3 输出:-1 示例 3 : 输入:coins = [1 ], amount = 0 输出:0 示例 4 : 输入:coins = [1 ], amount = 1 输出:1 示例 5 : 输入:coins = [1 ], amount = 2 输出:2 提示: 1 <= coins.length <= 12 1 <= coins[i] <= 231 - 1 0 <= amount <= 104
思路 首先就是使用递归,但是递归也是分情况的
穷举,把所有的可能都列出来,拿出最优解
寻找最小子问题,把这一个问题的最优解能用子问题解决
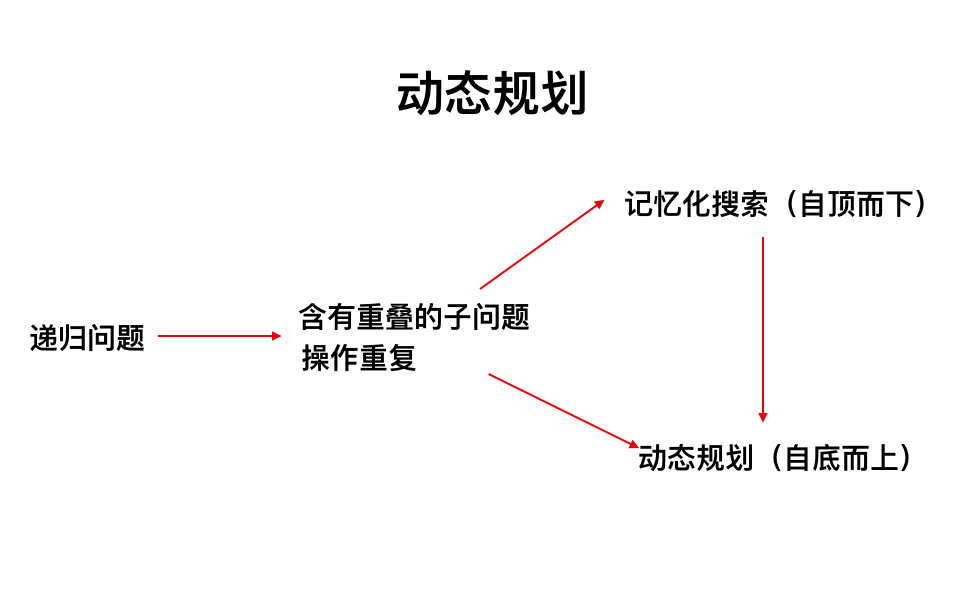
但是注意,如果我们想优化,也就是记忆化递归(也叫备忘录),这种情况的前提就是递归有子问题,而不是用的毫无规律的穷举。
而对记忆化递归再次优化,就是动态规划。
实现 穷举递归 这个是最初实现的,但是这个有很多的问题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 private static class Solution1 public int coinChange (int [] coins, int amount) if (amount == 0 ) { return 0 ; } int count = Integer.MAX_VALUE; count = getCount(coins, amount, 0 , 0 , count); return count == Integer.MAX_VALUE ? -1 : count; } private int getCount (int [] coins, int amount, int myCoin, int mycount, int count) if (myCoin > amount) { return count; } if (myCoin == amount) { count = Math.min(mycount, count); return count; } for (int coin : coins) { myCoin += coin; mycount++; if (mycount > count) { return count; } count = getCount(coins, amount, myCoin, mycount, count); mycount--; myCoin -= coin; } return count; } }
==这个是最容易想到的,也是我一步试出来的==
首先想到的就是,使用两个变量,一个是金钱金额的逐步累加值,一个是金钱次数的逐步累加值
然后穷举,不用管效率,把所有的问题都考虑到。
1 2 3 mycount--; myCoin -= coin;
原因:因为我把这个变量赋值了,这个值已经发生了改变所以必须要回溯,但是如果没有赋值,直接参数传递,那么就不需要回溯。
穷举优化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 private static class Solution1_1 int count = Integer.MAX_VALUE; public int coinChange (int [] coins, int amount) if (amount == 0 ) { return 0 ; } getCount(coins, amount, 0 , 0 ); return count == Integer.MAX_VALUE ? -1 : count; } private void getCount (int [] coins, int amount, int myCoin, int mycount) if (myCoin > amount) { return ; } if (myCoin == amount) { count = Math.min(mycount, count); } for (int coin : coins) { if (mycount > count){ return ; } getCount(coins, amount, myCoin + coin, mycount + 1 ); } } }
递归之子问题 一般我们递归都是寻找子问题,因为找到子问题才能找到记忆话递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 private static class Solution1_2 int res = Integer.MAX_VALUE; public int coinChange (int [] coins, int amount) if (coins.length == 0 ){ return -1 ; } findWay(coins,amount,0 ); return res == Integer.MAX_VALUE ? -1 :res; } public void findWay (int [] coins,int amount,int count) if (amount < 0 ){ return ; } if (amount == 0 ){ res = Math.min(res,count); } for (int i = 0 ;i < coins.length;i++){ findWay(coins,amount-coins[i], count+1 ); } } }
记忆化递归 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 private static class Solution3 public int coinChange (int [] coins, int amount) int [] vis = new int [amount]; if (amount < 1 ) { return 0 ; } return getCount(coins, amount, vis); } private int getCount (int [] coins, int amount, int [] vis) if (amount < 0 ) { return -1 ; } if (amount == 0 ) { return 0 ; } if (vis[amount - 1 ] != 0 ) { return vis[amount - 1 ]; } int min = Integer.MAX_VALUE; for (int coin : coins) { int res = getCount(coins, amount - coin, vis); if (res >= 0 && res < min) { min = res + 1 ; } } vis[amount - 1 ] = (min == Integer.MAX_VALUE ? -1 : min); return vis[amount - 1 ]; } }
动态规划 对记忆化递归的逆序,一般就是动态规划
如果能找到记忆化递归,那么就相当于找到了状态转移方程,那么就可以找到动态规划
在有状态转移方程后,动态规划的一般模板:
1 2 3 4 5 6 7 8 # 初始化 base case dp[0 ][0 ][...] = base # 进行状态转移 for 状态1 in 状态1 的所有取值: for 状态2 in 状态2 的所有取值: for ... dp[状态1 ][状态2 ][...] = 求最值(选择1 ,选择2. ..)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 private static class Solution4 public int coinChange (int [] coins, int amount) int [] vis = new int [amount + 1 ]; Arrays.fill(vis, amount + 1 ); vis[0 ] = 0 ; for (int i = 1 ; i <= amount; i++) { for (int coin : coins) { if (coin <= i) { vis[i] = Math.min(vis[i], vis[i - coin] + 1 ); } } } return vis[amount] > amount ? -1 : vis[amount]; } }