剑指 Offer 17. 打印从1到最大的n位数

题目

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]
 

说明：

用返回一个整数列表来代替打印
n 为正整数

原题目：

思路

普通的暴力解法就能够得到答案，但是这个题目原本要就是大数情况下的打印，这个n可以使无限大的。

所以这个时候不能用int去保存打印的数字，而是需要用string保存。

但是使用string也需要注意一点：

使用int类型时，每轮可以通过+1生成下一个数字，而此方法无法直接应用到string类型。并且，String类型的数字的进位操作效率较低，例如：“9999”进位到“10000”，需要从个位到千位循环判断，进位4次，效率较低。

所以最后的结果是通过String+全排列完成，避开进位操作，通过递归生成数字的String列表。

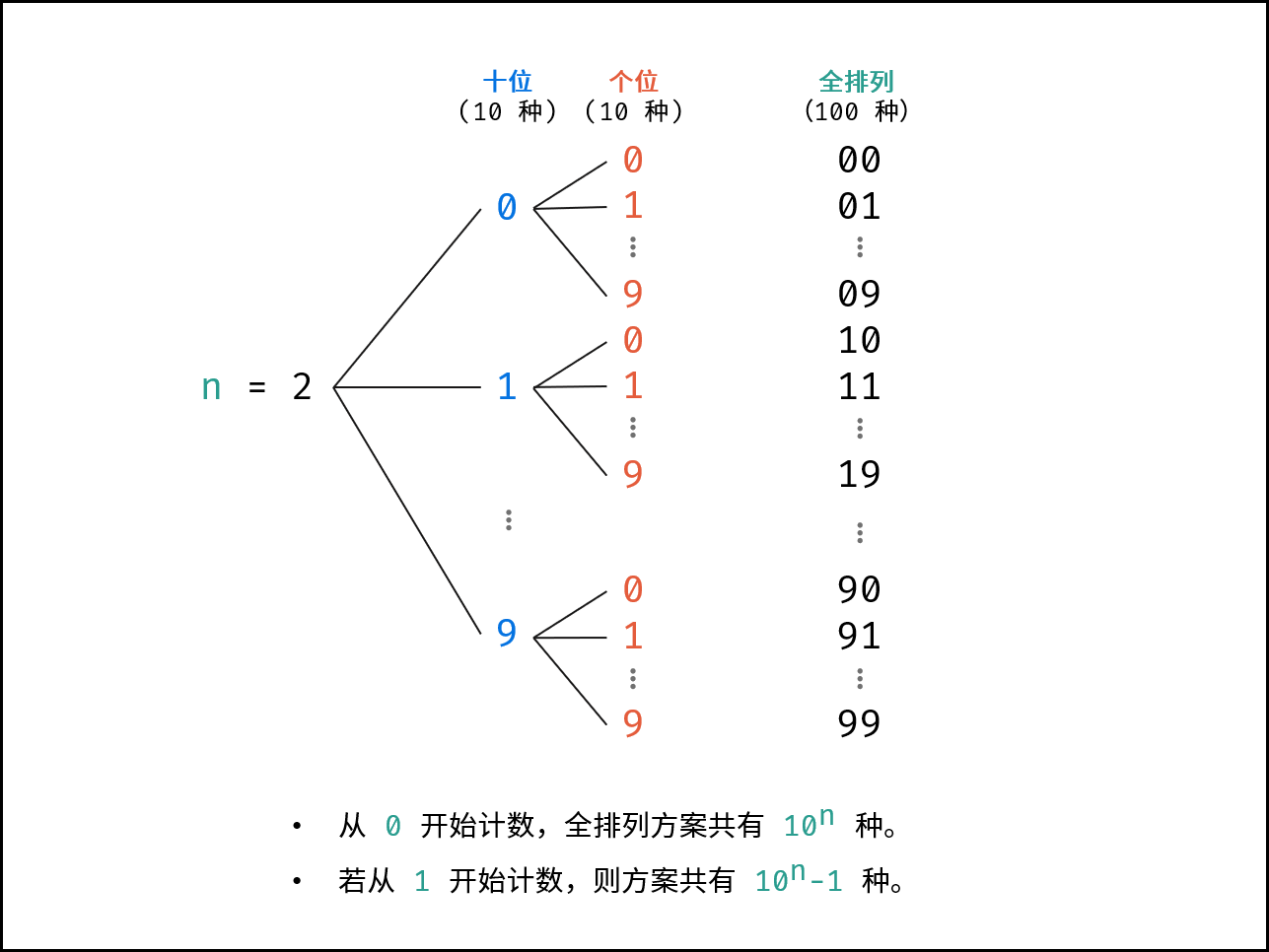
递归生成全排列：

基于分治算法的思想，先固定高位，向低位递归，当各位已被固定时，添加数字的字符串。例如：当n=2时（数字范围1-99），固定十位为0-9，按顺序依次开启递归，固定个位0-9，终止递归并添加数字字符串。

实现

暴力解法

public int[] printNumbers(int n) {
    // 这里也可以使用Math的pow方法
    //            int count = (int) Math.pow(10, n) - 1;
    int count = getCount(n);
    int[] res = new int[count];
    for (int i = 0; i < count ; i++) {
        res[i] = i + 1;
    }
    return res;
}

public int getCount(int n) {
    int x = 10;
    long b = n;
    double res = 1.0;
    while (b > 0) {
        if ((b & 1) == 1) {
            res *= x;
        }
        x *= x;
        b >>= 1;
    }
    return ((int) res - 1);
}

使用String的暴力解法

==注意一：如果将本题改为考虑int的范围，那么返回值应该是范围String类型的字符串==

==注意二：即便使用了string类型，在一般的电脑环境下还是会报错OOM，这种情况是考虑内存比较大的情况下，要不及时多少组的计算结果不断放入外存中==

这种直接调用string类型的“add方法”，效率低。

private static class Solution2 {
    public String printNumbers(int n) {
        // 定义bigInteger类型的变量，然后在此基础上++操作
        BigInteger num = new BigInteger("1");
        // res接收结果
        StringBuilder res = new StringBuilder();
        // 一直在num上++，终止条件是bum的个数小于传入的数字
        while (num.toString().length() <= n) {
            res.append(num).append(",");
            num = num.add(new BigInteger("1"));
        }
        // 最后要把多余的逗号删去
        res.replace(res.length()-1,res.length(),"");
        return res.toString();
    }
}

使用String类型的全排列

粗略

这种情况下生成的字符串，“001”，前面的0会显示，我们需要把前面的无意义的0全部去掉

注意：

这里的全排列和我们正常的那种dfs有稍微的区别，我们正常的全排列，需要判断这个数组中的数是否拿过，而这里的全排列是一个笛卡尔积，这个数还是可以取第二次的，所以我们不需要声明一个变量来判断该节点是否访问过。

private static class Solution3 {
    private int n = 0;

    public String printNumbers(int n) {
        this.n = n;
        char[] path = new char[n];
        char[] loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
        int depth = 0;
        StringBuilder res = new StringBuilder();
        // 注意这个不需要判断这个节点是否访问过
        dfs(depth, path, loop, res);
        res.replace(res.length() - 1, res.length(), "");
        return res.toString();
    }

    private void dfs(int depth, char[] path, char[] loop, StringBuilder res) {
        if (depth == n) {
            res.append(String.valueOf(path)).append(",");
            return;
        }
        for (char c : loop) {
            path[depth] = c;
            dfs(depth + 1, path, loop, res);
        }
    }
}

1 2	000,001,002,003,004,005,006,007,008,009,..... ....990,991,992,993,994,995,996,997,998,999

优化

我们这里主要是为了把前面的0去掉。

private static class Solution4 {
    private int n = 0;

    public String printNumbers(int n) {
        this.n = n;
        char[] path = new char[n];
        char[] loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
        int depth = 0;
        StringBuilder res = new StringBuilder();
        // 注意这个不需要判断这个节点是否访问过
        dfs(depth, path, loop, res);
        res.replace(res.length() - 1, res.length(), "");
        return res.toString();
    }

    private void dfs(int depth, char[] path, char[] loop, StringBuilder res) {
        if (depth == n) {
            // 主要是在这，对path遍历，如果前面的数字为0，则寻找下一个数字，知道找到一个非零的数字
            for (int i = 0; i < path.length; i++) {
                if (path[i] != '0'){
                    res.append(String.valueOf(path).substring(i)).append(",");
                    break;
                }
            }
            return;
        }
        for (char c : loop) {
            path[depth] = c;
            dfs(depth + 1, path, loop, res);
        }
    }
}